Certain syntactic constructs in a programming language are redundant and serve only the purpose of making life easier for the programmer: They are syntactic sugar. A good example is the augmented assign operator in many languages:
x += a which is just another way of writing x = x + a but is often more readable and works usually for any operator.
To implement this functionality you have several choices: Introducing a new AST node type with associated type checking / code generation functions would be one way. But that conflicts with DRY: Don’t repeat yourself.
A more elegant way of implementing augmented assignment is directly during parsing. ANTLR supports AST rewrites while parsing so instead of generating an (AUGASSIN (OP x a)) node we can create a normal assign node: (ASSIGN (x (OP (x a))))
If your parser does not support this kind of AST generation you can implement this idea in a additional compilation stage: AST postprocessing / desugaring. As I’ll show later in this post there are cases when the AST construction is complicated for some node types so that it’s preferable to use a general purpose programming language instead of doing this task inside ANTLR.
The idea is to traverse the AST looking for certain node types, here AUGASSIGN. If you see such a node you simply replace it with a new subtree which is functionally equivalent to the original node.
Problems with ANTLR
In the case of the Python ANTLR runtime it was not that easy. I could not transform the AST at will without conforming to the special API of the tree implementation. Maybe it’s just me but I think it’s somewhat inconvenient to work with.
So the first step was to convert the AST from the ANTLR format to my own really simple tree implementation. I just copied the node type, text and line / character position information and all children recursively.
AST Visualizer
Before going deeper with the discussion of AST postprocessing I’ll present two of my tools here to visualize an abstract syntax tree. These make debugging the parser and desugar code much easier.
My first program creates a dot file from the AST. The dot file format is a human readable description of directed and undirected graphs. dot files can be displayed using several tools: For example using the dot command line utility you can generate a png which you can open with your favorite image viewer.
Here is the code that generates the contents of the dot file:
def AST2DOT(ast):
def idGen():
i = 0
while True:
yield i
i += 1
r = ['digraph G\n{']
def walk(t, idGen):
selfI = idGen.next()
label = []
label.append('<')
label.append('<table border="0" cellborder="0" cellpadding="3" bgcolor="white">')
label.append('<tr><td bgcolor="black" align="center" colspan="2"><font color="white">%s</font></td></tr>' % t.text)
def createRow(s1, s2=''):
return '<tr><td align="left">%s</td><td align="left">%s</td></tr>' % (s1, s2)
label.append(createRow('%s, %s' % (t.line, t.charPos)))
label.append('</table>')
label.append('>')
label = ''.join(label)
r.append('n%d [ label=%s, style="filled, bold" penwidth=5 fillcolor="white" shape="Mrecord" ];' % (selfI, label))
n = t.getChildCount()
for x in range(n):
c = t.getChild(x)
ci = walk(c, idGen)
r.append('n%d -> n%d' % (selfI, ci))
return selfI
walk(ast, idGen())
r.append('}')
return '\n'.join(r)
This is somewhat limited since the generated graphs get large really fast and so this approach is not suitable for source files of more than a few lines of code. Of course it’s still possible to display only small sub trees.
Here’s a sample from my Exoself test suite:
module t013
def(mangling=C) puts(_ as byte*) as int32;
def main() as int32
{
s as byte*;
s = ar"Much simpler hello world!";
puts(s);
puts(ar"Hallo Welt!");
return 0;
}
And the resulting AST:
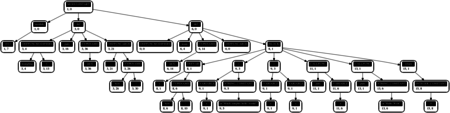
AST for 013_strings.es. Click for full size.
My second ast viewer is a small pygtk dialog with a tree view to browse through larger graphs:
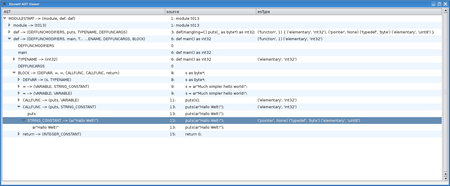
Interactive AST viewer. Click for full size.
Both methods are really simple and invaluable for debugging. (If you know any good tools for interactive directed graph visualization where nodes can be expanded / collapsed please write a comment – it should run on Linux and be able to display huge, as in thousands of nodes, graphs)
More postprocessing
A problem which is not easy to solve in ANTLR was implementing the AST for functions which are used as binary operators:
function_operator: atom (NAME atom)+;
Suppose you have two functions subtract and multiply which each accept two arguments of type int32. What does the following code do?
9 subtract 3 multiply 3
In Exoself this expression is executed from left to right. First subtract(9, 3) is calculated and the result is 6. Now multiply(6, 3) is evaluated so the final result is 18. So we want to construct an AST that reflects this order of function calls:
(CALLFUNC (multiply (CALLFUNC (subtract 9 3)) 3))
Now let’s review the ANTLR code for parsing this expression again, now with AST rewrite:
function_operator: a+=atom
(
/* nothing */ -> $a
| (n+=NAME a+=atom)+ -> ^(FUNCTIONOPERATOR $n+ $a+)
);
Since I could not find a simple way to express the target AST using AST rewrites I just accumulate all function names and expressions into the variables a and n and expand them in the AST node again. The transformation is then done in my AST post processing phase.
Some more examples where this technique is useful
while COND {...} else {...}
The else should be executed only if the while body is not executed at least once. It’s just syntactic sugar for an if around the while and exactly that does my desugarer.
if COND {while COND {...}} else {...}
x[5][1][3]
Array subscripts have the same problem as function operators. The evaluation order can’t be expressed easily using AST rewrites.
a = b = c = 42
Exoself allows variables to be defined by assignment. So lets assume that b is a float64 and a / c are not defined yet.
As the type of 42 is by default int32 the variable c is defined with this type and assigned the value 42. Now the variable b is assigned 42 after an implicit conversion to float64. In the next step a is assigned the value of b. Thats the float64 42.0 and not the integer 42, so a is of type float64.
A bit complicated to implement? Not really. Just transform the AST to the following code:
c = 42; b = c; a = b;
Often this technique makes it much easier to implement the next compilation phase – but at the cost of some overhead. You usually have to at least traverse the whole AST in every phase, so for larger trees this can be significant.
The next post (posts?) will be about semantic analysis. I’ll discuss some ideas how to implement a type system for a language similar to C (but with stronger typing) and additional information we need to add to the AST to generate code in the following step.